研究内容について教えてください

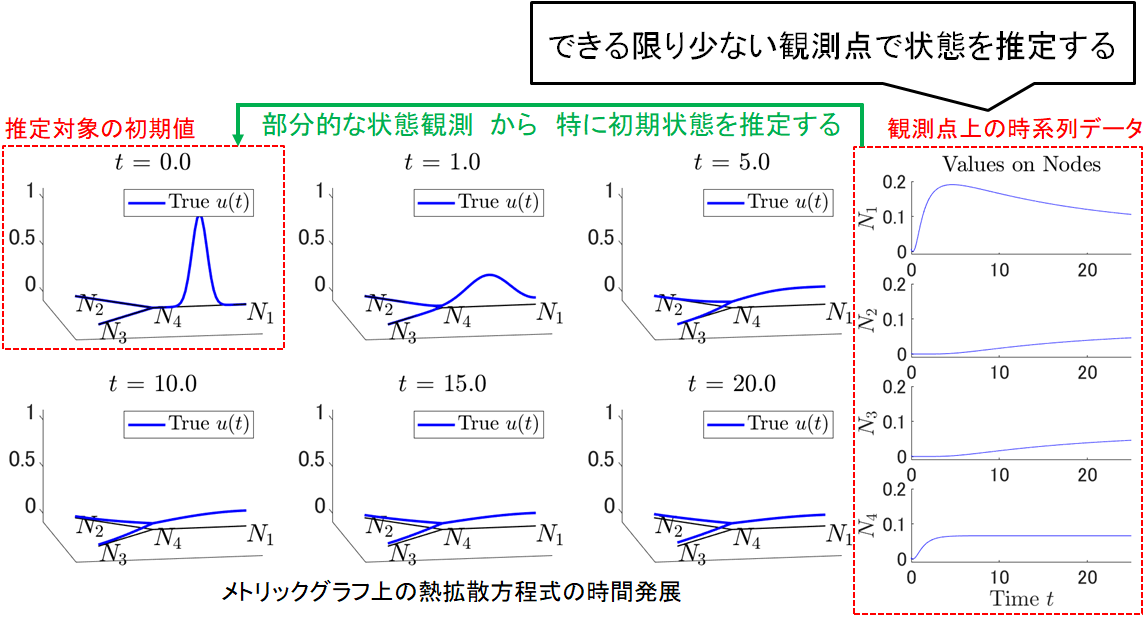
例えば、室内の任意の1か所の温度を観測します。時間や湿度など様々な条件が変化すると、温度も変化します。各条件と温度の変化の関係を方程式で説明することができれば、同じ部屋の別の場所の温度も、各条件を方程式に代入することで、観測することなく知ることができます。

このように、ある現象を説明する方程式を解き明かし、同一条件下で発生する現象を復元しようと試みているのが、私が取り組んでいるテーマ「偏微分方程式における縮約理論に基づくサロゲートモデルの構築」です。サロゲートモデルとは、ある現象について理解する際、従来のように実験などの物理シミュレーションを行う代わりに、現象を方程式で表現し、AIなどを使って仮想シミュレーションを行う手法です。

サロゲートモデルが構築できれば、冒頭のように「同空間の異なる場所の温度を方程式から割り出す」ということが可能です。サロゲートモデルは、例えば溶鉱炉の検査などに応用が可能です。溶鉱炉は一旦起動すると、寿命を迎えるまで停止できません。当然ながら溶鉱炉の内部は超高温の溶けた鉄で満ちていますから、炉の内部も周辺も高温で人が検査することはできません。そこで、溶鉱炉の正常稼働している箇所の温度変化を観測し、方程式化します。その方程式を利用すれば、温度変化を知るだけで各箇所が正常に稼働しているかどうかが分かるのです。実現すれば、温度センサーを炉の各箇所に配置するだけで、炉の内部が正常な状態か自動で分かるので、人間が危険な作業をする必要がなくなります。
同様にサロゲートモデルが構築できれば、地中に埋設された配管の管理やコンピューター内の微細な電子回路の動作チェックなどにも応用ができます。

サロゲートモデルの正確性を向上させるには、変化に関係する条件を可能な限り網羅し、各条件の変化を考慮した方程式を作らねばなりません。「部屋の任意の場所の温度を知る」場合でも、サロゲートモデルを構築する方程式を作るために、時間、気温や湿度、天候、部屋の容積などなど様々な条件が関わってきます。1つでも条件が変われば、方程式は変わります。サロゲートモデルの構築が、とても困難であることが理解していただけると思います。

現実世界では、全てが同一の条件下で事象が発生することはまずありませんから、万能なサロゲートモデルの構築は不可能に近いと言えます。サロゲートモデルは、「物理シミュレーションの代替になるもの」ではなく、「物理シミュレーションと共に使うことでシミュレーション全体の精度を上げるもの」と考えてバランス良く両方を活用することが重要です。

説明のため応用可能な例を挙げましたが、私が行っているのはあくまで理論の研究です。現状では企業と連携して実際に装置を作るといった取り組みは行っていません。ですが、世の中のあらゆる現象を数式で解明することに挑戦する、大きな可能性にあふれた研究だと自負しています。今この瞬間は世の中で活用されることは難しいとしても、研究を前進させなければ活用される未来は訪れない。「打席に立たねば、ヒットは打てない」と考え、日々研究に励んでいます。

この研究を始められたのはいつからですか？

現在の研究室に移り、研究を始めたのは最近のことです。以前は現在とは逆のアプローチの研究を手がけていました。現象を方程式で解き明かすのではなく、すでに分かっている方程式で現象を再現し、応用する研究です。
アプローチの方向性は正反対ですが、どちらも「世の中の現象を数式で解明しようとする研究」という点は同じ。ペンと紙があればできる。現在ならPCやタブレットがあれば研究が進められる。いつでもどこにいても、常に考え続けられる研究、という意味でも同じですね。

研究室を移ったと言いましたが、前研修室と今の研究室は、大阪大学のISTの施設の中でたまたま隣同士。研究のアプローチは逆になりましたが、私の通勤経路や研究の環境にはほぼ変化はありませんでした。